Francesco Macrì: Algoritmi per il calcolo di media e varianza

Introduzione

In statistica la varianza di una variabile aleatoria X è un numero, indicato con Var(X), o $\sigma^2$ , che fornisce una misura di quanto i valori assunti dalla variabile differiscano dalla media µ. In altri termini è il valore medio del quadrato degli scarti. La varianza è quindi una misura di concentrazione: minore (maggiore) è la varianza, peggiore (maggiore) è la concentrazione (dispersione) dei dati attorno al valore medio.

La formula matematica per il calcolo della varianza per un’intera popolazione di dimensione N è:

$\sigma ^2=\frac{1}{N}[\sum_{i=1}^{N}x_{i}^2-\frac{1}{N}(\sum_{i=1}^{N}x_{i})^2]$

La formula per il calcolo di una stima corretta della varianza di un campione di grandezza n è invece:

$S^2=\frac{1}{n-1}[\sum_{i=1}^{n}x_{i}^2-\frac{1}{n}(\sum_{i=1}^{n}x_{i})^2]$

Algoritmi

Gli algoritmi per il calcolo della varianza svolgono un ruolo importante nel calcolo statistico. Uno degli algoritmi per calcolare la media e la varianza è il cosiddetto Algoritmo Naive:

Quest’algoritmo può essere utilizzato per il calcolo della varianza per un’intera popolazione semplicemente dividendo per N invece che per n-1 nell’ultima riga.
Poiché Sum_sqr e (Sum*Sum)/n possono essere numeri molto simili, questo potrebbe portare ad avere una varianza molto vicina allo 0 e quindi ad una poca precisione del risultato.
Un algoritmo alternativo a quello appena presentato prevede l’utilizzo di due step separati per il calcolo della varianza:
1) calcoliamo la media del campione: $\overline{x}=\frac{1}{n}\sum_{i=1}^{N}x_{i}$
2) calcoliamo la somma dei quadrati della differenza dalla media: $s^{2}=\frac{1}{n-1}\sum_{i=1}^{n}\left(x_{i}-\overline{x} \right )^2$

Il codice utilizzato per il Two Step Algorithm è il seguente:

Quest’algoritmo è sempre numericamente stabile, a meno che n non sia troppo elevato.
Entrambi gli algoritmi calcolano la differenza tra due somme di grandi dimensioni simili tra loro. E’, dunque, poco conveniente utilizzarli nella pratica, in quanto sono estremamente vulnerabili agli effetti dell’arrotondamento nelle operazioni con numeri a virgola mobile; è, infatti, facile incorrere ad errori computazioni come la Catastrophic Cancellation che prevede la cancellazione di molte cifre significative. E’ possibile ottenere, in alcuni casi, varianza negativa!
Gli algoritmi precedenti possono, però, essere migliorati.

Il problema della perdita di cifre significative è descritta e analizzata da Donald Knuth (Art of Computer Programming, Vol 2, Seminumerical Algorithms“, section 4.2.2), un informatico statunitense. La soluzione prevede di calcolare media e varianza utilizzando equazioni di ricorrenza nel caso di data stream:

$\overline{x}_{n}=\frac{(n-1)\overline{x}_{n-1}+x_{n}}{n}$

$\sigma^{2}_{n}=\frac{(n-1)\sigma^{2}_{n-1}+(x_{n}-\overline{x}_{n-1})(x_{n}-\overline{x}_{n})}{n}$

Dalle precedenti equazioni possiamo ricavare anche la formula di ricorrenza per la covarianza:

$\sigma^{2}_{xyn}=\frac{(n-1)\sigma^{2}_{n-1}+(x_{n}-\overline{x}_{n})(y_{n}-\overline{y}_{n-1})}{n}$

È di notevole interesse la dimostrazione che dalle formule classiche portano alla scrittura delle formule di ricorrenza:

Media:
$\overline{x}_{n}=\frac{\sum_{i=1}^{n}x_{i}}{n}=x_{n}+\frac{\sum_{i=1}^{n-1}x_{i}}{n}=x_{n}+(n-1)\overline{x}_{n-1}$

Varianza: $\sigma ^{2}_{n}=\frac{\sum_{i=1}^{n}(x_{i}-\overline{x}_{n})^{2}}{n}=\frac{\sum_{i=1}^{n}x_{i}^{2}- n\overline{{x}}^{2}_{n}}{n}$ .

Consideriamo la differenza 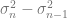$\sigma^{2}_{n}-\sigma^{2}_{n-1}$ :

$\sigma^{2}_{n}-(n-1)\sigma^{2}_{n-1}=$
= $\sum_{i=1}^{n}x_{i}^{2}-n\overline{x}_{n}^{2}-\sum_{i=1}^{n-1}x_{i}^{2}+(n-1)\overline{x}_{n-1}^{2}$
= $x_{n}^{2}-n\overline{x}_{n}^{2}+(n-1)\overline{x}_{n-1}^{2}$
= $x_{n}^{2}-\overline{x}_{n-1}^{2}+n(\overline{x}_{n-1}^{2}-x_{n})(\overline{x}_{n-1}+\overline{x}_{n})$
= $x_{n}^{2}-x_{n}\overline{x}_{n}-x_{n}\overline{x}_{n-1}+x_{n}\overline{x}_{n-1}$
= $(x_{n}-\overline{x}_{n})-(x_{n}-\overline{x}_{n-1})$

da cui $\sigma ^{2}_{n}=\frac{\sum_{i=1}^{n}(x_{i}-\overline{x}_{n})^{2}}{n}=\frac{\sum_{i=1}^{n}x_{i}^{2}- n\overline{{x}}^{2}_{n}}{n}$ .

I “running Algorithm” (o algoritmi online) sono quegli algoritmi che utilizzano le formule appena dimostrate. Essi vengono attribuiti da Knuth a Welford.

Considerando la quantità $M_{2,n}=\sum_{i=1}^{n}(x_{i}-\overline{x}_{n})^2$ , riportiamo di seguito il codice dell’algoritmo online:

Quest’algoritmo è molto meno incline alla perdita di precisione dovuta alla cancellazione, ma potrebbe essere meno efficiente a causa dell’operazione di divisione all’interno del ciclo.

Esempio

Di seguito riportiamo un codice per il calcolo della media, della varianza e della covarianza implementati in VB.NET e in C# considerando due liste a priori.
Mettendo i due codici dei due linguaggi a confronto risultano essere molto simili tra loro.
Calcolo della media in VB.NET:

Calcolo della media in C#:

Calcolo della varianza in VB.NET:

Calcolo della varianza in C#:

Per il calcolo della covarianza bisogna definire un’altra lista in quanto la covarianza è una misura di quanto due variabili aleatorie variano assieme, ovvero al loro dipendenza:

Calcolo della covarianza in VB.NET: